최근 바이오 분야에서도 빅데이터의 바람이 불고 있습니다. 데이터가 범람하는 시대에서 데이터의 직관적 이해는 어느 날보다도 중요해지고 있고, 이를 위해서는 인간의 인지 수준을 넘어선 높은 차원의 데이터를 낮은 차원으로 시각화하는 기법이 필요할 것입니다. 이러한 기법을 차원축소(Dimension Reduction)라고 합니다.
가장 대표적으로 사용되는 알고리즘은 주성분 분석(Principal Component Analysis, PCA)입니다. 저명한 통계학자 Pearson에 의해 1901년에 최초로 소개된 만큼 꽤 오랜 역사를 지니고 있습니다. 주성분 분석은 주어진 차원과 데이터의 진정한 차원이 다를 수 있다는 문제의식에서 시작했습니다.
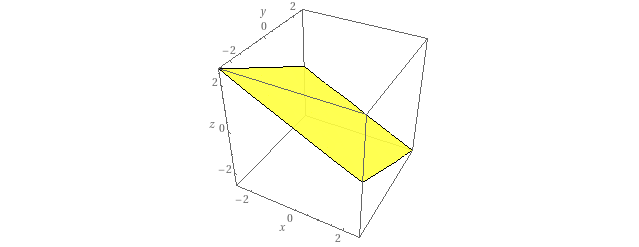
데이터들이 위와 같이 노란색 평면 상에 놓여 있다고 생각하면 주어진 차원은 3차원이지만 데이터의 진정한 차원은 2차원이 될 것입니다. 이때 주어진 차원의 기저(Basis)는 예를 들면 다음과 같이 나타낼 수 있습니다.
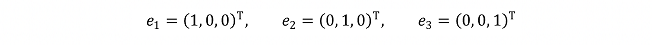
참고로, 위와 같이 꼭 직교할 필요는 없습니다. 또한, 데이터의 진정한 차원의 기저는 다음과 같이 나타낼 수 있습니다.
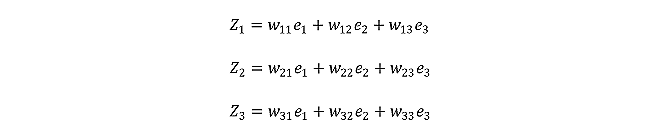
위와 같은 기저는 무한히 많을 것입니다. 이때 정규성 (계수의 크기가 1인 성질), 최선성 (분산량이 많은 기저를 더 빠른 순위로 하는 것), 직교성 (서로 서로 내적이 0인 성질)을 모두 고려하는 것이 PCA 알고리즘입니다.
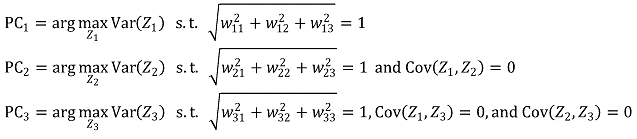
이러한 문제를 푸는 방법은 크게 세 가지가 있습니다. 첫 번째 방법은 고유값, 고유벡터를 이용하는 방법입니다. 다음과 같이 Variance-Covariance Matrix ∑를 정의하여 n번째로 큰 고유값에 대한 고유벡터를 n번째 주성분으로 취하는 것입니다.

구체적인 계산과정은 여기에 있습니다. 이때 세 번째 주성분은 가장 정보량이 적은 주성분인 만큼 주어진 평면의 법선벡터와 일치함을 확인할 수 있습니다. 한편, 두 번째 방법은 등식제약 하에서의 라그랑주 승수법을 사용하는 것입니다. 이는 해석학적 개념을 많이 요하므로 여기를 참고합니다. 마지막 세 번째 방법은 Center Matrix에 대한 Singular Value Decomposition(SVD)을 시도하는 것으로, 최적화 알고리즘이 많이 이루어져서 현재 PCA 알고리즘의 표준 방법으로 채택되고 있습니다.
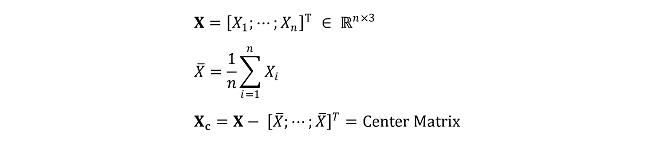
만약 주어진 데이터가 n차원이라면 n개의 주성분이 나오게 됩니다. 그런데 n개의 주성분 전부가 의미있는 것은 아니라서 적당한 개수 k < n개만 추후 분석에 이용하게 됩니다. 이때, Eigen Value에 대한 Scree Plot, Fraction of Total Variance에 대한 Scree Plot, Minimum MSPE 등 다양한 기준을 활용합니다.
이렇듯 차원축소는 기본적으로 데이터의 Redundant한 정보를 제거하는 과정으로 볼 수 있습니다. 이를 통해 여러 가지 부수적인 효과가 발생하고, 이들 효과로 인해 PCA 등의 차원축소 알고리즘이 오늘날까지도 사랑받고 있습니다.
Take Home Message
1. 차원축소는 주어진 고차원 데이터를 시각화하는데 유리하다.
2. 차원축소는 머신러닝에 있어 속도를 높이고 부하를 줄인다.
3. 차원축소는 데이터의 노이즈를 감소시킨다.
4. 차원축소는 데이터의 진정한 차원을 알게 해준다.
이상 포트래이 tech 블로그였습니다.





